annafone.blogg.se - Superposition principle circuits examples

SUPERPOSITION PRINCIPLE CIRCUITS EXAMPLES SERIES

It is an important concept to determine voltage and current across the elements by calculating the effect of each source individually. The Superposition Theorem is used to solve complex networks with a number of energy sources. Steps to Follow for Superposition Theorem.It’s worth noting that the superposition theorem doesn’t apply to power because it isn’t a linear quantity. A positive sign in the total indicates that a contribution from a source is in the same direction as the reference direction a negative sign indicates that it is in the opposite direction.Īll of the components of a circuit must be linear to employ the superposition theorem with currents and voltages.

Each unknown quantity should be assigned a reference direction. When adding up each source’s individual contributions, be careful when assigning signs to the quantities.

The superposition theorem demands the presence of two or more sources in the circuit.

When only one source is considered at a time, power dissipation is a nonlinear function that does not add up to an accurate total algebraically. Because linearity is required, the Superposition Theorem can only be used to calculate voltage and current, but not power.

Non-linear circuits are not covered by the theorem.

V.After you’ve gotten the results for each individual source, add them all up to get the overall voltage drop or current across the circuit element. Iv.The same applies to all other sources in the circuit when evaluating a single source. Iii.Evaluate the current flowing through or the voltage drop across a specific network node using a network simplification approach. Ii.All sources must be changed by their internal impedance, with the exception of the specified source. Any one of the circuit’s multiple sources can be taken into consideration initially. I.The initial step is to choose one source among the many available in the bilateral network. The voltage sources can be eliminated by shorting their two terminals, and the current sources can be eliminated by opening their two terminals. As a result, the remaining independent sources must be removed from the circuit. Only one independent source will be considered at a time in this procedure. It asserts that when numerous independent sources act at the same time in a linear circuit, the response in that branch is equal to the total of the responses owing to each independent source acting at a time. The assumption of linearity between the response and excitation of an electrical circuit underpins the superposition theorem. A sound system is an example of linear circuit-based electronic equipment. Linear circuits are advantageous because they can enhance and process electronic signals with minimal distortion.

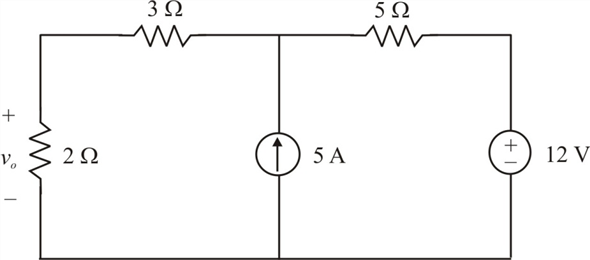
When the voltage or current in the circuit is increased, the values of electronic parts (such as resistance, capacitance, inductance, gain, and so on) do not change.

SUPERPOSITION PRINCIPLE CIRCUITS EXAMPLES SERIES

This eliminates the need to write a series of loop or node equations, making calculations easier. When numerous independent sources are present, the voltages and currents created by each can be calculated independently and then added algebraically. Any linear circuit can benefit from the superposition theorem. Linear circuitĪ linear circuit is an electrical circuit that operates on the superposition principle. It only applies to circuits that meet the ohm’s law requirements (i.e., for the linear circuit). In other words, if a number of voltage or current sources act in a linear network, the total current in any branch is the algebraic sum of all the currents that would be produced if each source acted independently while all the other independent sources were replaced by their internal resistances. When two or more sources are present and connected, the superposition theorem is utilised to solve the network. According to the superposition theorem, the response across each element in a linear, active, bilateral network with more than one source is the sum of the responses obtained from each source evaluated independently, and all other sources are replaced by their internal resistance.